La "invención" o el "descubrimiento" del número cero fue, en cierta forma, una consecuencia de la adopción del sistema posicional de numeración. Probablemente el símbolo 0 para representar el cero es de origen griego, pero mucho antes los babilonios y los hindúes tenían ya maneras de nombrarlo y representarlo. Donde quiera que haya sido que primero se aceptó el cero como un número tan legítimo como el ocho o el doscientos doce, allí nació la matemática moderna.
El cero es el signo numérico de valor nulo, que en notación posicional ocupa los lugares donde no hay una cifra significativa. Si está situado a la derecha de un número entero, decuplica (multiplica por diez) su valor; colocado a la izquierda, no lo modifica.
Utilizándolo como número, se pueden realizar con él operaciones algebraicas como: sumas, restas, multiplicaciones, entre otras. Pero, por ser la expresión del valor nulo (nada, nadie, ninguno..), puede dar lugar a expresiones indeterminadas o que carecen de sentido.
Es el elemento del conjunto ordenado de los números enteros (ℤ, ≤) que sigue al –1 y precede al 1. Algunos matemáticos lo consideran perteneciente al conjunto de los naturales (ℕ) ya que estos también se pueden definir como el conjunto que nos permite contar el número de elementos que contienen los demás conjuntos, y el conjunto vacío tiene ningún elemento. El número cero se puede representar como cualquier número más su opuesto (o, equivalentemente, menos él mismo): X + (–X) = 0.
El cero posicional
La civilización india es la cuna de la notación posicional, de uso casi universal en el siglo XXI. La palabra «cero» proviene de la traducción de su nombre en sánscrito shunya (vacío) al árabe sifr (صفر), a través del italiano. La voz española «cifra» también tiene su origen en sifr.
Es posible que el matemático indio Brahmagupta (siglo VI) fuera el primero en teorizar sobre el concepto de "cero" no sólo como definición de una cantidad nula, sino como posible sumando para números negativos y positivos. El primer testimonio del uso del «cero indio» está datado en el año 683: una inscripción camboyana de Angkor Wat, tallada en piedra, que incluye el número "605".
Otras pruebas de uso se datan hacia el año 810. Las inscripciones de Gwalior están datados en 875-876. Abu Ja'far Mujammad ibn Musa (Al-Juarismi), en su obra titulada «Tratado de la adición y la sustracción mediante el cálculo de los indios» explica el principio de numeración posicional decimal, señalando el origen indio de las cifras. La décima figura, que tiene forma redondeada, es el «cero»
Los árabes lo transmitieron por el Magreb y Al-Ándalus, pasando posteriormente al resto de Europa. Los primeros manuscritos que muestran las cifras indias (llamadas entonces «árabes») provienen del norte de España y son del siglo X: el Codex Vigilanus y el Codex Aemilianensis. El cero no figura en los textos, pues los cálculos se realizaban con ábaco, y su uso aparentemente no era necesario.
Aunque se atribuyen los primeros usos del cero en Francia, o al controvertido papa Silvestre II, alrededor del año 1000, la mayor parte de las referencias indican que el cero (llamado zefhirum) fue introducido en Europa por el matemático italiano Fibonacci en el siglo XII, mostrando el álgebra árabe en su Liber abaci (El libro del ábaco), aunque por la facilidad del nuevo sistema, las autoridades eclesiásticas lo tildaron de mágico o demoníaco.
La iglesia y la casta de los calculadores profesionales —clérigos en su mayoría, que utilizaban el ábaco— se opusieron frontalmente, vetando la nueva álgebra, en algunos lugares hasta el siglo XV.
Representaciones del cero
El cero se representa en textos occidentales con el signo numérico «0». Desde el siglo XX, y especialmente con el desarrollo de la informática, es frecuente que este signo aparezca cortado por una barra diagonal (/), nueva notación que evitaba la confusión con la grafía de la letra «o». Hasta hace poco, la conjunción disyuntiva o debía llevar tilde: «ó», cuando iba escrita entre cifras para no ser confundida con el signo numérico 0. Actualmente, dicha regla no está en vigor.
Representación gráfica del cero
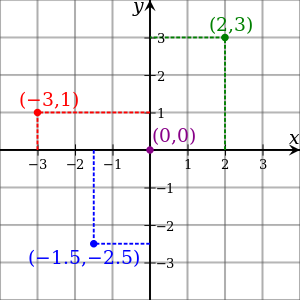
En coordenadas cartesianas el origen de coordenadas se asocia al valor 0 (cero).
El cero y los números naturales
El cero, por ser un concepto numérico especial, no se incluía en el conjunto de los números naturales ℕ, por convenio. Y se representaba como ℕ0, al conjunto de los números naturales cuando incluye al cero, por ello es posible encontrar muchos libros donde los autores no consideran al cero como número natural. De hecho, aún no hay consenso al respecto.
A algunos matemáticos les resulta conveniente tratarlo como a los otros números naturales, por eso la discrepancia. Desde un punto de vista histórico el cero aparece tan tarde que algunos no creen que sea justo llamarlo natural.
Operaciones matemáticas con el cero
El cero en la suma
En la suma, el cero es el elemento neutro; es decir, cualquier número a sumado con 0 vuelve a dar a. Ejemplo:
25 + 0 = 25.
El cero en la resta
En la resta, el cero es el elemento neutro; es decir, cualquier número a restado con 0 vuelve a dar a, excepto cuando el cero es el minuendo, en cuyo caso resulta -a. Ejemplos:
37 – 0 = 37
0 - 37 = -37
El cero en la multiplicación
En el producto, el cero es el elemento absorbente; cualquier número operado con 0 da 0. Ejemplo: 25 × 0 = 0
El cero en la división
Entre las controversias que existen sobre el cero, una de ellas es sobre la posibilidad de dividir por él; pero el cero puede dividir a otros números, en cuyo caso es el elemento absorbente (ejemplo: 0:25 = 0). El problema es que se utiliza la misma palabra, división, para referirse a distintas cosas (aunque en el fondo tengan el mismo origen).
División por cero en los números reales
En los números reales (incluso en los complejos) la división entre cero es una indeterminación; así, las expresiones:
8/0; 0/0
carecen de sentido.
Intuitivamente, significa que no tiene 'sentido' «repartir» 8 manzanas entre niños de un aula vacía. Tampoco tiene 'sentido', distribuir 0 billetes entre cero personas: nada entre nadie. Matemáticamente, el cero es el único número real por el cual no se puede dividir. Por eso 0 es el único real que no tiene inverso multiplicativo. Ejemplo:
x/2 = x · 1/2 (correcto).
x/0 = x · 1/0 (incorrecto porque 1/0 no es un número real).
El cero en la potenciación
- Si a es distinto de 0, entonces a0 = 1 → 90 = 1
- Si a es mayor de 0, entonces 0n = 0 → 04 = 0
Por qué el cero es par
Es fácil probar directamente que el cero es un número par.- Se dice que un número es par si es un múltiplo entero del 2. Entonces, por definición, el cero es par:
2 x 0 = 0.
Esta demostración comienza con una definición estándar de "número par". También es posible explicar por qué el cero es par sin hacer mención a definiciones formales. Las explicaciones siguientes deben ser comprendidas en términos fundamentales de conceptos de números.
Pares | Impares |
 | |
Fundamentos
El conteo básico utiliza números. Dado un conjunto de elementos, es común utilizar números para describir cuántos objetos hay en el conjunto. Cero es la cuenta de ningún objeto; en términos más precisos, es el número de objetos que hay en el conjunto vacío. El concepto de paridad es utilizado al formar grupos de dos objetos: si los objetos de un conjunto pueden agruparse de a dos, sin dejar ninguno sin pareja, entonces el número de objetos del conjunto es par; si un objeto queda aislado, entonces el número de objetos del conjunto es impar.
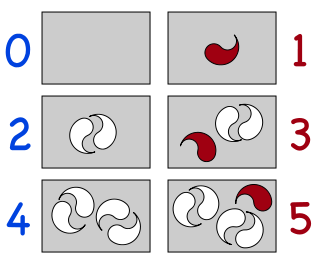
El conjunto vacío contiene cero grupos de dos, y ningún objeto queda aislado con este agrupamiento. No es evidente sin embargo visualizar cero elementos de dos, o poner atención en la no-existencia del objeto aislado; esta concepción de la paridad del cero puede ser ilustrada al comparar al conjunto vacío con otros conjuntos, como en el diagrama de la derecha, en donde la caja con 0 elementos no tiene objetos sin pareja, como la que tiene dos y la que tiene cuatro. En las cajas en las que sí hay elementos sin pareja estos están en rojo (las que tienen uno, tres y cinco).
La recta numérica permite una visualización más uniforme de los números, incluyendo los números positivos, los números negativos y al cero. Cuando los pares y los nones se destacan visualmente, el patrón se vuelve evidente:
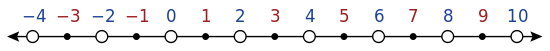
Los pares y los impares se alternan. Un conteo de derecha a izquierda o de izquierda a derecha comenzando en un número par, siempre incluye el cero, y no hay ninguna razón para excluirlo. Y un conteo de derecha a izquierda o de izquierda a derecha comenzando en un número impar, excluye siempre el cero, y no hay ninguna razón para incluirlo.
Paridad
En el conjunto de los enteros ℤ, el 0 es un número par; satisface la definición de paridad, así como también todas las características de los números pares.
La definición precisa de un término matemático, tal como «par significa entero múltiplo de dos» es, en última instancia, una convención. Algunos términos o definiciones matemáticas se construyen explícitamente para excluir casos triviales. Los números primos constituyen un conocido ejemplo; la definición de "número primo" ha variado históricamente de "entero positivo con a lo sumo 2 factores" a "entero positivo con exactamente 2 factores", con el notable efecto de que el 1 ya no se puede considerar primo. La mayoría de los autores hacen notar que esta definición conviene mejor a los teoremas matemáticos que conciernen números primos. Por ejemplo, el teorema fundamental de la aritmética es más cómodo de enunciar si el 1 no se considera primo.
De modo análogo, sería posible redefinir el término «par» de manera que no incluyera al cero. Sin embargo, en este caso, la nueva definición haría más difícil establecer teoremas concernientes a los números pares. Los efectos pueden notarse, por ejemplo, en las leyes que gobiernan la aritmética de los números enteros pares e impares:
- par ± impar = par
- impar ± impar = par
- par × entero = par
Al hacer una excepción con el cero en la definición, estas reglas serían incorrectas y tendrían que ser, cuando menos, modificadas. Por otra parte, respetar las leyes obedecidas por los números pares positivos, y requerir que sigan siendo válidas para todos los enteros, fuerza la definición usual y la consecutiva paridad del cero.
Y, por último, hay una afirmación que no necesita ser demostrada: Todo número terminado en cero es par.
| Volver al índice |